小白：师兄，上次听你讲了李群李代数，有种“听君一席话胜读十年书”的赶脚~后来看书感觉容易理解多了呢！

师兄：是吗？那太好啦，给你讲的过程也加深了我的理解呢

小白：那师兄今天要不要继续加深理解一下相机成像模型 的部分呢？

师兄：额。。好啊（感觉被套路了，不过想想上次小白师妹请客吃了烧烤呢）

小白：讲完一起吃饭去~

师兄：好呀好呀！

小孔成像

师兄：相机成像模型我们主要介绍针孔相机。中学时我们都学过小孔成像，还记得吧。像下面这个图，就是小孔成像示例。你看三维空间的蜡烛在带有小孔的黑箱子里成像一个倒立是像，这个是实像

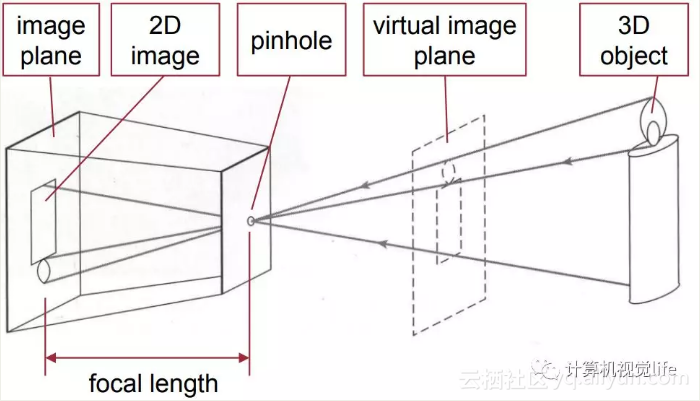
小白：嗯嗯，还有印象，那个正立的虚线画的就是虚像吧

师兄：是的。话说几千年前人们就发现了这个现象了~

小白：那师兄为啥要画这个虚像呢？

师兄：因为这个虚像和实像是完全对称的，数学上可以等价，后面我们推导公式的时候比较方便。

小白：这样啊，还有个问题，为啥我看好多书上提到相机模型都是讲的针孔相机？

师兄：因为自然界中这个成像过程最普遍，我们普通的相机，视场角不太大的话都符合针孔相机成像模型

小白：可是，普通相机好像没有针孔那么小。。。

师兄：哈哈，这个针孔是个类比，比如手机摄像头镜头相对于被拍摄物体到手机的距离就非常小了，可以近似为一个针孔的

小白：糗大了。。。

师兄：没事，不懂就问不能不懂装懂嘛。我们继续，前面针孔相机用数学表达就是下面这样。我们把倒立的实像去掉，用正立的虚像代替就行啦。三维空间的点大P在成像平面上成的像就是小p了。大P，小p还有相机中心C在同一条直线上。

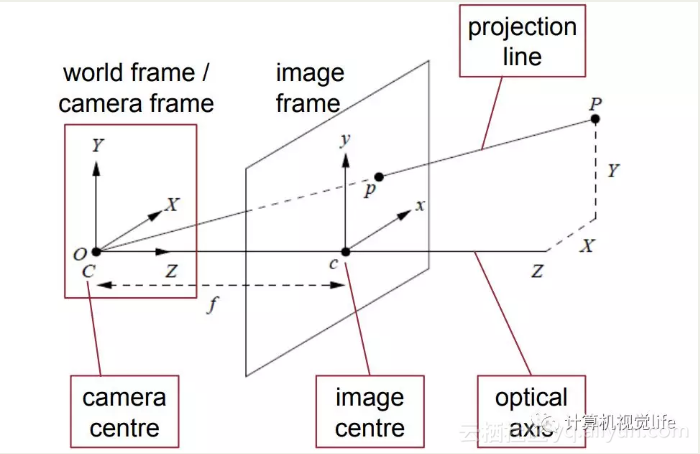
小白：嗯，这个图还挺直观的

纷繁复杂的坐标系

师兄：下面我们即将进入公式的世界，yeah~

小白：师兄，我数学是语文老师教的。。。尽量通俗易懂的讲哈

师兄：嗯，第一步，我们先要明白，这个三维空间有好多坐标系，一个，两个。。大概有三四个吧。

小白：（捂脸）

师兄：首先说两个，世界坐标系和相机坐标系。顾名思义：

世界坐标系(world coordinate system)：就是用户定义的三维世界的坐标系，以某个点为原点，为了描述目标物在真实世界里的位置而被引入。单位为m。

相机坐标系(camera coordinate system)：就是以相机为原点建立的坐标系，为了从相机的角度描述物体位置而定义，作为沟通世界坐标系和图像/像素坐标系的中间一环。单位为m。

小白：师兄，你说的好学术啊，这俩有啥不一样？

师兄：举个栗子吧。比如姚明要开始100米跨栏了，我们可以定义那个起点就是世界坐标系原点。。

小白：打住。。。姚明好像是打篮球的吧？

师兄：哦哦，对，说错了，是刘翔在世界坐标原点（在师妹面前糗大了）。那么，那么那个拍照的摄影师，对，那个摄影师假如是姚明，那么姚明所在的位置就是相机坐标系的原点，这时候刘翔在相机坐标系中就不是原点了。

小白：理解~

师兄：我们举个普通的例子，比如下面这个图，最右上方的那个点在三维空间中，如果以世界坐标系为原点，它的坐标就是Xw，如果以相机坐标系为原点，它的坐标就是Xc，我们可以通过旋转R和平移t来把世界坐标系转换到和相机坐标系重合

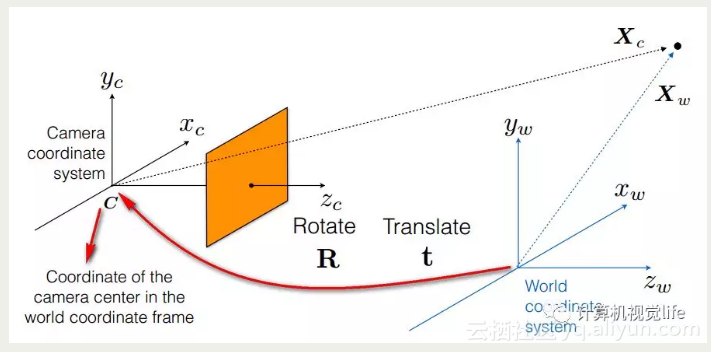
小白：这个R，t就是之前我们讲过的变换矩阵吧

师兄：对啊，如果用数学公式表示的话，就是下面这个啦，我们在《》还讲了为什么要使用齐次坐标，还记得吧？

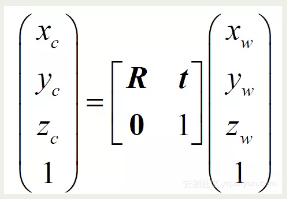
小白：记得呢，我有复习过的哦（顿时感觉自己也没有那么小白了），嘻嘻

师兄：不错。这个R,t 为就是相机的外部参数，一般用T表示，这个参数随着相机的移动而变化。下面我们假设已经把世界坐标系变换到相机坐标系下了。

我们再来说一下图像坐标系(image coordinate system)吧，它是为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入，是我们真正从相机内读取到的图像所在的坐标系。单位为像素。

针孔相机成像原理

我们来看看下面这个图吧。相机坐标系下的点P(X, Y, Z)在相机成像平面上成的像为P'(X', Y', Z')

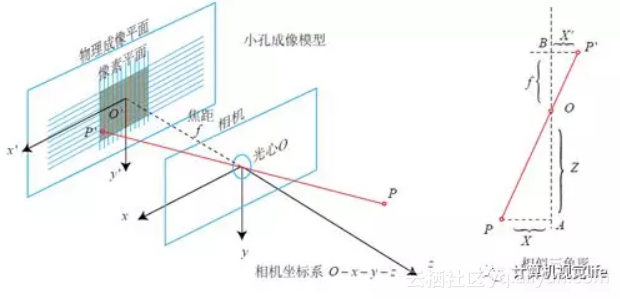
那么根据三角形相似原理，如右图所示，能推导出如下式子

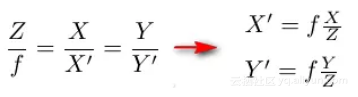
其中，f是相机的焦距。

小白：嗯，这个三角形相似还有印象，这个式子看懂了

师兄：但是成像过程一般是以图像中心点为坐标系原点的，如下图所示。而我们做图像处理的时候习惯于从左上角为图像坐标系原点，所以。。

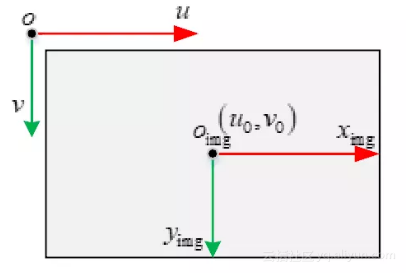
小白：所以还需要一个平移？

师兄：恭喜，你都会抢答啦！下面式子中cx, cy就是分别在x,y方向的平移，一般是长和宽的一半。

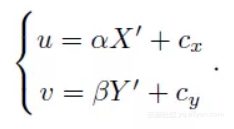
小白：师兄，好好的为什么要平移啊？

师兄：哦，这是因为虽然成像的时候是以图像中心为原点，但是我们图像存储的时候都是从左上角开始存储的，这样方便数据的读写

小白：原来是这样啊！除了平移外，还有个尺度因子α，β，这个尺度因子从哪里冒出来的？！

师兄：你想想，前面X', Y'单位是什么？cx, cy单位是什么？

小白：X', Y'单位应该和X,Y 类似，是（毫）米吧，cx, cy是图像坐标系的，我们一般说图像多少多少像素，那单位应该是像素吧？

师兄：没错！所以需要尺度因子统一一下单位，所以尺度因子α，β单位是像素/（毫）米，这样和X',Y'相乘后单位就是像素啦！

小白：是哦，这样就可以直接和cx, cy相加啦！等我默念一般哈：

X', Y'单位是 毫米

α，β单位是像素/（毫）米

cx, cy单位是像素

好啦，师兄继续吧~

师兄：有了前面两个式子，我们把第2个带入第1个，就得到了下面式子，u, v都是图像坐标系下坐标，单位是像素

小白：这个公式看懂啦！不过我看书上都写成矩阵的样子了啊

师兄：没错，一般都写成齐次坐标，用矩阵表示，如下图

左侧图像坐标是齐次坐标，中间红色框内的矩阵K称为内参数，最右侧蓝色框内的就是相机坐标系下的三维点P啦！

小白：写成矩阵形式真的挺方便的！

师兄：对，你看还有一个1/Z 的系数，这个Z是相机坐标系下P点的Z坐标，如果把这个 1/Z 和 P(X,Y,Z) 进行相乘，就得到了相机坐标系下P的归一化坐标 P = (X/Z, Y/Z, 1)， 它位于相机前方z =1 的平面上。

小白：原来这就是归一化坐标说法的来源啊！

师兄：对，我们结合前面从世界坐标系到相机坐标系的变换，就有了如下式子：

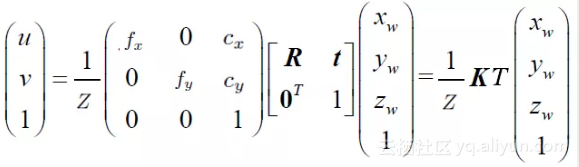
其中 fx, fy 分别是x, y方向焦距，一般都是相等的, cx,cy是光心位置，一般是长和宽的一半，他们都叫内参，此外还有畸变系数也属于内参，他们都是相机固有参数。

到此，针孔相机成像模型就讲完啦！

小白：嗯，感觉很有收获！

师兄：总结一下整个过程：

1、首先，世界坐标系下有一个三维点Pw

2、若世界坐标系到相机坐标系下的变换为旋转矩阵 R 和平移向量t 组成的变换矩阵 T，那么Pw在相机坐标系下的坐标为 Pc = R*Pw + t = T*Pw

3、此时的Pc三个分量分别是X, Y, Z，我们需要把它投影到归一化平面Z=1上，这样我们得到了相机坐标系下Pc的归一化坐标 Pc' = (X/Z, Y/Z, 1)

4、用内参矩阵乘以归一化坐标就得到了像素坐标 Puv = K*Pc'

小白：嗯，这下彻底明白啦！

相机畸变

小白：师兄，那个畸变参数还没讲呢！

师兄：哦对，这个畸变参数也很重要的，也是内参的重要组成。

小白：师兄，为啥相机会畸变啊？

师兄：这是因为我们的相机前面有个透镜，如果想要相机一次性拍摄很大的范围，像下面这个图这样，就需要把透镜做的中间很厚两边薄，这样光线经过透镜后会发生折射，相机就能看到更多物体啦。不过这样的话，我们前面的针孔模型中的那些三角形相似的假设就不能满足啦！

也就是说：畸变产生的原因是：透镜不能完全满足针孔模型假设

小白：嗯，好像是这样，那种鱼眼相机看起来就是凸的很呢，拍出来图片边缘的房子都扭曲了。是不是所有相机都是一种类型的畸变啊？

师兄：不是的，相机透镜的畸变主要分为径向畸变和切向畸变，还有其他的畸变，但都没有径向和切向畸变影响显著，所以我们在这里只考虑径向和切向畸变。

小白：啥是径向啥是切向啊？

师兄：你看下面这个图，很形象。这是径向畸变的两种类型，一种是桶形，像个木桶，一种是枕形，像个枕头

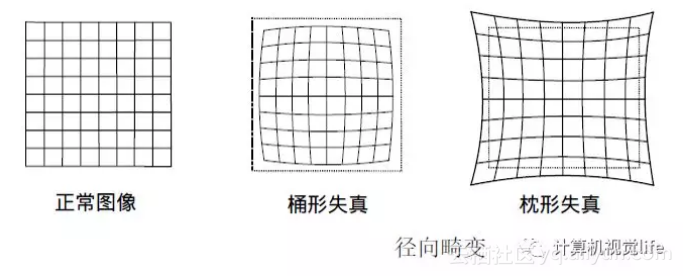
小白：真的很像哎，哈哈

师兄：你看他们的畸变程度有什么特点？

小白：好像中间部分还好，越往周围扭曲越严重？

师兄：是，畸变程度都是从中心开始，用一个半径画圆的话，半径越大，圆周上的畸变程度也越大。这个就是由于相机透镜的形状导致的，且越向透镜边缘移动径向畸变越严重。

小白：嗯，挺直观的，那切向畸变是啥？

师兄：切向畸变是由于透镜和CMOS或者CCD的安装位置误差导致。看下面的图，因此，如果存在切向畸变，一个矩形被投影到成像平面上时，很可能会变成一个梯形。不过随着相机制造工艺的大大提升，这种情况很少出现了，我们一般也不考虑切向的畸变。

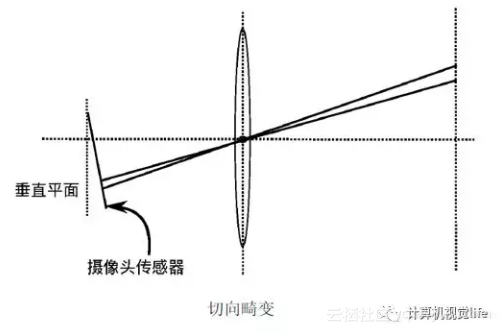
小白：那就是说只要考虑径向畸变就行了？（不用学切向畸变了，yeah！）

师兄：对。下面我们来说说怎么样对畸变进行去除

小白：感觉很难的样子。。。

师兄：是有点麻烦。首先需要对相机进行标定，标定完就能得到相机的所有内参，包括畸变系数。我们用标定的畸变系数就能对畸变的图像进行去畸变啦

小白：那这个相机标定怎么做的？

师兄：这个还是挺复杂的，标定的原理你可以看看一个叫“计算机视觉life”的公众号，里面讲相机标定原理还是挺清楚的~

小白：嗯，师兄，记住啦，我去关注一下。

师兄：假设我们已经标定好了，下面来看看如何用畸变系数来去畸变吧

小白：好啊，这个感觉很神奇啊

师兄：对，你看下面式子就是去畸变的公式，记住这个就行了。你看等式左边都是拍摄的原图的坐标，就是发生了畸变的。

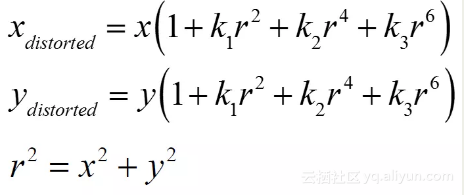
小白：下标的distorted出卖了它，哈哈

师兄：嗯，等式右边的坐标x, y是去畸变后的图像坐标，它是归一化的坐标，以图像中心为原点，还有那个r 就是半径啦，你看这是一个圆的方程。你觉得这个怎么计算出 x, y？

小白：感觉这个计算好像很麻烦啊，左边是已知，右边是未知，再带进去那个半径，天呐，没法想象啊！

师兄：确实如你所说，如果是正常的思维方式，确实很难解。不过，我们可以反过来算，就简单多了

小白：怎么反过来？

师兄：就是我们假设已经有了去畸变的图像了，对应下面左图，它的坐标 x, y自然已经知道了，然后带入右边式子，最后得到一个x_distorted, y_distorted的坐标，这个坐标对应的就是扭曲的图里的坐标，就是下面右图，我们只要把这个像素值替换掉去畸变的图片里的 x, y 处像素值就好啦！

小白：这个好神奇哦

师兄：嗯，很巧妙的方法。不过计算得到的 x_distorted, y_distorted可能不是整数，是一个浮点数，这就需要进行插值计算了。

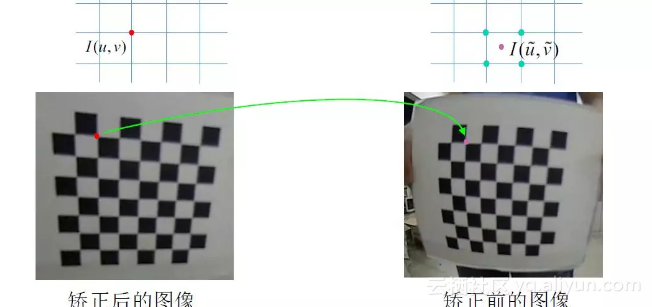
小白：具体怎么做呢？感觉还是有点晕呢

师兄：这个就是留给你的作业了，你自己做一遍，就不晕啦！

小白：（我晕。。）

原文发布时间为：2018-10-30

本文作者：electech6

本文来自云栖社区合作伙伴“”，了解相关信息可以关注“”。